이전 글에서 전도대 안의 전자밀도 공식을 공부해보았다.
같은 방식으로 가전대 안의 정공밀도도 구할 수 있다. 즉, 가전대 안의 정공밀도는 아래의 공식으로 주어진다.

여기서 E_v , E_v b는 각각 가전대의 가장 위의 에너지 준위와 가전대의 가장 아래의 에너지 준위를 나타낸다.
그리고 정공은 전자가 없는 상태이므로 Fermi-Dirac분포함수는 [1-f(E)] 로 주어진다.
전자밀도를 구했을 때 처럼 같은 방식으로 적분구간은 -∞ 에서 0 으로 근사할 수 있다.
이에 따라 위의 적분식을 계산하면

와 같이 구해진다. 여기서 N_v는 정공에 대한 유효상태밀도이다.

진성반도체에서는 전자와 정공의 수가 같으므로 n = p = n_i 이다. 따라서 진성반도체에서의 Fermi 준위(E_F)는

와 같이 구해진다. 진성반도체의 Fermi 준위는 전도대(E_c)와 가전대(E_v)의 중간에 위치함을 볼 수 있다.
앞에서도 말했듯이 진성반도체에서는 n = p = n_i 이므로

와 같은 관계식을 얻을 수 있다. 이를 질량작용의 법칙(mass action rule)이라고 부른다.
이 관계식을 이용하면 어떤 반도체에서 전자밀도를 알면 정공밀도를 알 수 있고, 거꾸로 정공밀도를 알면 전자밀도를 알 수 있다.
n형 반도체에서 상온에서 모든 도너 원자들은 이온화되며, 이에 따라 각 도너 원자들은 전자를 내어 놓는다.
n형 반도체의 전도대에 존재하는 전자에는 도너 원자에 의해 제공되는 전자와, 가전대에서 올라오는 전자가 있다.

따라서 n형반도체의 전도대에서의 전자밀도 n = n_i + N_d 로 주어진다. 이전에 말했듯이 N_d ≫ n_i 이므로
n = N_d 라고 볼 수도 있다.
p형 반도체에서 상온에서 모든 어셉터 원자들은 이온화되며, 이에 따라 각 어셉터 원자들은 정공을 발생시킨다.
p형 반도체의 가전대에 존재하는 정공에는 어셉터 원자에 의해 제공되는 정공과 가전대에서 전도대로 올라간 전자에 의해 만들어지는 정공이 있다.

따라서 가전대에서의 정공밀도 p = n_i + N_a 로 주어진다. 이전에 말했듯이 N_a ≫ n_i 이므로
p = N_a 라고 볼 수 있다.
n형 반도체에서 다수캐리어(majority carrier)는 전자이고 소수캐리어(minority carrier)는 정공이다.
반면에 p형 반도체에서 다수캐리어는 정공이고, 소수캐리어는 전자이다.
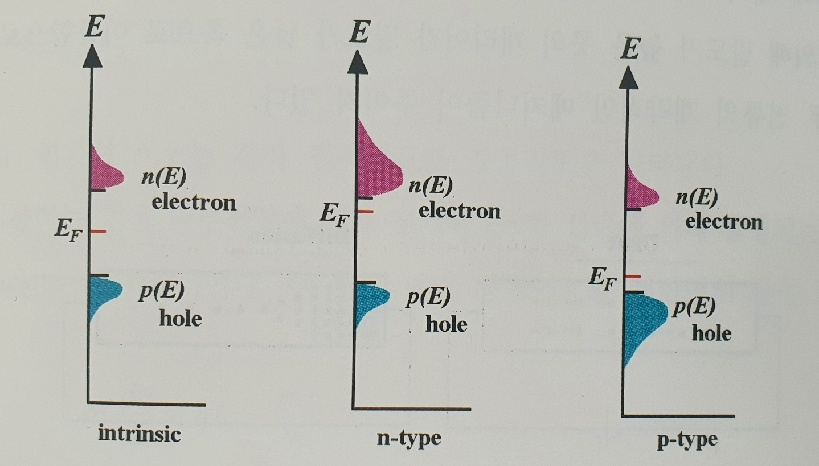
진성반도체와 n형 반도체와 p형 반도체 각각에서 다수캐리어, 소수캐리어 밀도 분포 모양을 보여주고 있다.
진성반도체는 전자와 정공의 분포가 같은것을 확인할 수 있다.
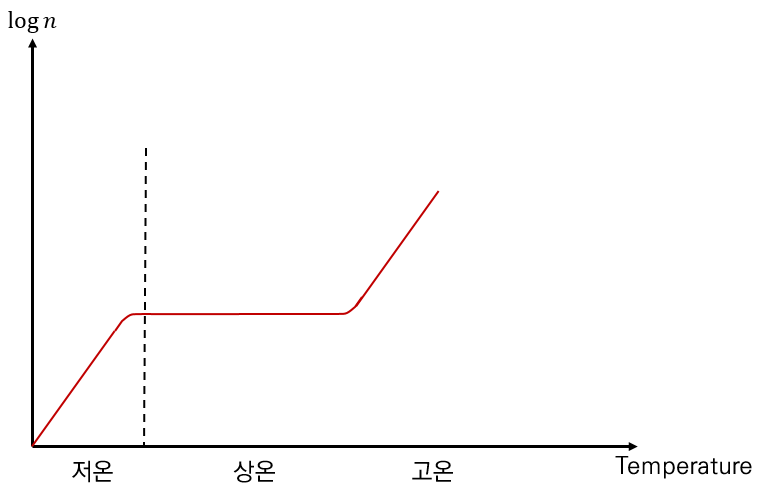
저온에서는 소수의 도너 원자들만이 이온화 된다. 온도가 증가함에 따라 이온화되는 도너 원자들이 많아져서 전도대의 전자밀도가 증가하게 된다. 이 영역을 진성반도체 영역이라고 부른다.
상온에서는 모든 도너 원자들이 이온화되므로 전자밀도는 온도에 따라 변하지 않고 일정하게 된다.
고온에서는 가전대의 전자들이 전도대로 올라갈 수 있으므로 전자밀도가 다시 증가한다.
이러한 전자밀도의 온도에 따른 변화는 저항의 온도에 따른 변화와 반대이다.
'과학도를 위한 반도체와 전자회로의 기초' 책을 공부하여 작성 하였습니다.
'self.반도체&전자회로 공부' 카테고리의 다른 글
| [pn접합의 특성] pn 접합이란? 다이오드 (0) | 2022.03.23 |
|---|---|
| [반도체의 특성] 캐리어에 의한 전류밀도 (0) | 2022.03.22 |
| [반도체의 특성] 반도체 캐리어(Carrier) 밀도_1 (0) | 2022.03.20 |
| [반도체의 특성] 진성반도체와 외인성반도체 (0) | 2022.03.18 |
| [반도체의 정의] 반도체 기초 지식, 에너지 밴드 (1) | 2022.03.17 |



