이전에 n형 반도체와 p형 반도체 각각의 캐리어인 전자와 정공의 밀도를 공부해보았다.
2022.03.20 - [self.반도체&전자회로 공부] - [반도체의 특성] 반도체 캐리어(Carrier) 밀도_1\
전류밀도
반도체에서 전류는 드리프트(drift) 전류와 확산(diffusion) 전류로 구성되어 있다.
드리프트 전류는 양단에 걸린 전압에 의해 캐리어가 이동함으로써 발생한다. 반면에 확산전류는 위치에 따른 캐리어 밀도의 차이에 의해 밀도가 높은 곳의 캐리어가 밀도가 낮은 쪽으로 이동함으로써 발생한다.

외부 전압이 걸려 있지 않은 반도체 내의 캐리어들도 열에너지에 의한 운동 때문에 격자나 불순물들과 끊임없이 충돌한다. 이러한 충돌에 의한 산란 때문에 캐리어의 속도의 크기와 방향은 계속 바뀐다.
그러나 이러한 산란은 무작위 산란이기 때문에 전체적으로 캐리어의 특정 방향으로의 이동은 없다.
반면에 외부 전압이 걸리면 캐리어들은 여전히 격자와 불순물 등과의 충돌에 의해 산란되지만 전체적으로 전기장 방향으로 이동하는 것을 볼 수 있다.
이러한 캐리어의 이동속도를 드리프트 속도(drift velocity)라고 부른다. 이 드리프트 속도는 외부 전압에 의해 형성되는 전기장에 비례하는데 그 비례 상수를 이동도(Mobility)라고 부른다.

길이가 L인 반도체에 전하 Q가 평균 드리프트 속도 v로 이동한다고 가정하자. 이 경우 L = vt, t = L/v 로 쓸 수 있고
그래서 전류 I는 Q/t = Qv/L 로 주어진다.
그리고 전류밀도는 단위면적당 전류로 정의되므로 J = I/A = Qv/AL = ρv라고 할 수 있다. 여기서 ρ는 전하밀도를 말한다.
따라서 캐리어가 전자, 정공인 경우 전류밀도는 각각 다음 식으로 표현된다. (n은 전자밀도, p는 정공 밀도)

드리프트 전류밀도
캐리어에 작용하는 힘은 외부 전압에 의한 전기력 qE와 산란에 의해 발생되는 운동량 변화에 따른 산란력(scattering force)이다. 산란력은 운동량을 산란 시간으로 나눈 값으로 표현할 수 있고,
전기력과 산란력 두 힘은 반대 방향이므로 캐리어의 운동 방적식은 아래와 같이 주어진다.

평형상태(steady state)에서는 캐리어가 이미 가속되어 일정한 평균속도에 도달한 상태이다. 따라서 dv/dt = 0 으로 둘 수 있다.
이에 따라

그래서 전체 캐리어의 드리프트 전류밀도는

로 정리할 수 있다.
확산 전류밀도
확산 전류는 캐리어 밀도의 차이에 의해 발생하므로 전자의 경우 확산전류밀도는 아래와 같이 정의할 수 있다.

위 식에서 dn/dx < 0 이고 전류의 방향은 전자의 방향과 반대이니까 이렇게 캐리어가 전자인 경우에는 전자의 확산 방향과 전류는 반대방향이라고 할 수 있다.
그리고 정공의 확산전류밀도는 아래와 같이 정의할 수 있다.
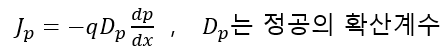
위 식에서 dp/dx < 0 이고, 이 경우에는 캐리어가 정공이기 때문에 전류의 방향과 확산 방향이 동일해야 한다. 그래서 - 부호가 붙은 것이다.
총 전류밀도
반도체에서 총 전류밀도는 [드리프트 전류밀도] + [확산 전류밀도] 이다. 그래서 반도체에서 전자와 정공에 의한 총 전류밀도는 각각
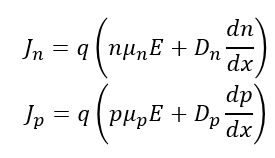
으로 정리된다.
| 이동도 | 확산계수 | |||
| 전자 | 정공 | 전자 | 정공 | |
| 실리콘 | 0.14 | 0.05 | 0.0036 | 0.0013 |
| 게르마늄 | 0.38 | 0.18 | 0.0098 | 0.0047 |
300K (상온, 26℃) 에서 대표적 반도체에서의 캐리어의 이동도와 확산계수 표 이다. (출처 : 과학도를 위한 반도체와 전자회로의 기초)
300K (상온, 26℃) 에서의 캐리어의 이동도와 확산계수를 보면 전자가 정공보다 드리프트도 쉽고 확산도 쉽다는 것을 알 수 있다.
캐리어의 확산계수와 이동도는 서로 관련이 되어있다. 이동도가 좋다면 확산도 잘 되기 때문이다. 확산계수와 이동도는 Einstein 관계식으로 연관되어있다.
온도 T에서 평형상태에 있는 캐리어들이 전압 V에 놓일 경우 캐리어 밀도를 지난 글에서 정리했었는데 그 식들을 Fermi 준위를 에너지의 기준으로 잡아서 표현하면 아래와 같다.
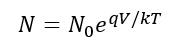
여기서 N은 전자일 경우 n, 정공일 경우 p를 나타낸다. 그리고 q는 전자일 경우 -e, 정공일 경우 +e 이다.
캐리어 밀도의 위치에 따른 변화는 먼저 위 식을 미분하면
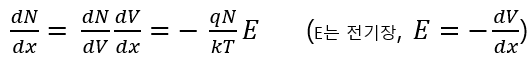
이렇게 표현할 수 있고 평형상태에서는 총 전류밀도(드리프트 전류 밀도와 확산 전류 밀도의 합)가 0 이므로 위에서 구한 총 전류밀도 식이 0 이 되어야 한다.

이를 아인슈타인 관계식(Einstein 관계식)이라고 부른다. 이 관계식에서 보듯이 확산 계수 D는 이동도와 비례하는 것을 알 수 있다.
'과학도를 위한 반도체와 전자회로의 기초' 책을 공부하여 작성 하였습니다.
'self.반도체&전자회로 공부' 카테고리의 다른 글
| [pn접합의 특성] pn 접합의 물리적 성질, 다이오드의 평형상태 (0) | 2022.03.24 |
|---|---|
| [pn접합의 특성] pn 접합이란? 다이오드 (0) | 2022.03.23 |
| [반도체의 특성] 반도체 캐리어(Carrier) 밀도_2 (0) | 2022.03.21 |
| [반도체의 특성] 반도체 캐리어(Carrier) 밀도_1 (0) | 2022.03.20 |
| [반도체의 특성] 진성반도체와 외인성반도체 (0) | 2022.03.18 |



