
RF Matching System과 스미스차트에 대하여(Smith Chart) - 2
지난 글에서 RF poewr의 임피던스와 Matching System이 필요한 이유에 대해 공부해보았다.
2022.07.27 - [self.반도체&전자회로 공부] - RF Matching System과 스미스차트에 대하여(Smith Chart) - 1
RF Matching System과 스미스차트에 대하여(Smith Chart) - 1
RF Matching System와 스미스차트에 대하여(Smith Chart) - 1 반도체 공정 중 Plasma를 사용하여 진행하는 공정이 있고, 그 Plasma를 생성하기 위해서 꼭 필요한 조건 중 하나가 바로 Power다. 그리고 RF power를..
selfimprove39.tistory.com
이번에는 Matching system을 스미스 차트를 이용하여 이해하기 위해 Smith Chart에 대해 공부해보자.
먼저 스미스 차트를 보자. 전기전자 전공이 아니어서 그런건지... 차트가 굉장히 복잡하고 어려워 보인다.

스미스 차트란?
스미스 차트는 1939년 필립 스미스가 전송 선로(Transmission line)의 편리한 계산을 위해 고안한 것으로, 복소임피던스를 시각화한 원형의 도표이다. ... 각종 결과를 스미스 차트로 출력해 봄으로써 전송 선로의 행동특성을 파악할 수 있어 아직까지 업계에서 널리 사용되고 있다.
위키백과, 스미스 차트
위키백과에 나온 스미스 차트의 설명을 다시 자세히 읽어보자.
일단 전송선로는 전자기파(전기적 신호)를 전송하기 위해 설계된 특수한 케이블이나 전기 도체로 만들어진 구조물을 말하는데, 지금 중요한 내용은 아니다.
중요한것은 복소 임피던스를 시각화 했다는 것이고, 전송 선로의 행동특성을 파악할 수 있다는것이다.
반사계수와 부하 임피던스와의 관계식을 정리해보면 복소수의 원의 공식으로 변환이 가능하고, 이것을 단계별로 그려 정리하면 된다.
또 이런 설명이 있는데, 스미스 차트는 임피던스와 반사계수의 관계를 나타내는 차트라는 것을 알 수 있다.

지난 글에서 임피던스는 저항보다 큰 개념이고, 크기와 위상을 갖는 값이라 복소수로 표시된다는 설명을 했었다.
복소수의 허수 부분을 직교 좌표계에서 표현할 때 사방이 무한대로 뻗어나가기 때문에(음의 값도 있으니까)
매우 큰 값의 임피던스를 표현해야 한다면 표시하기가 애매할 수 있다.
스미스 차트는 원형 좌표계로 표현함으로써 그 무한대의 위치까지 비선형 형태로 원 안에 다 표현할 수 있게 되었다.

임피던스의 실수 / 허수의 수치변화가 스미스 차트 내에서 임의로 움직이는 것이 아니라 그려진 궤적형상과 동일하게 이동한다는 점을 통해 계산기 없이도 여러 복소변화 계산을 가능하게 한다.
Z_L은 부하의 임피던스, Z_0은 전송 선로의 임피던스를 가리킨다.
여기서 RF matching 이란, Z_L과 Z_0의 임피던스를 같게 해준다는것이고 (Z_L = Z_0)
즉, 그 비율이 1이 된다는 것이다. (Z_L/Z_0 = 1)
스미스차트의 정 중앙 점이 바로 그 비율이 1이 되는 곳이고 임피던스가 50Ω 으로 같아지는 지점이다.(대부분 50Ω 이라서)
그래서 RF power를 사용하는 장치에서 원 위의 점을 정 중앙으로 이동시키는것이 임피던스 매칭이고,
그렇게 효율적으로 power를 사용하게 해주는 장치가 지난 글에서 공부한 RF matcher 이다.
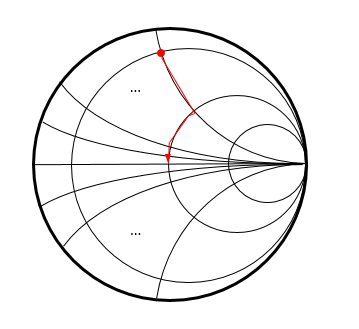
스미스 차트 해석
스미스 차트에서 좌표를 읽는 방법에 대해서는 자세히 쓰여 있는 글이 많아서 많은 도움이 되었다.
자세하게 읽는 방법 보다는 의미하는 바가 무엇인지에 초점을 맞추어 공부를 해보았다.
오른쪽의 한 점에서부터 시작되는 원은 복소 임피던스 값의 실수부이고,
동일한 한 점에서부터 시작되는 곡선이 허수부를 나타낸다.
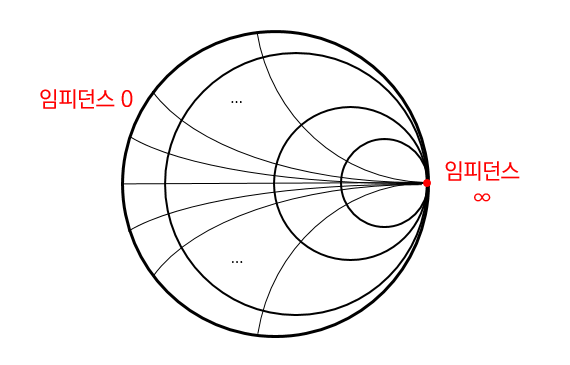
원이 모이는 한 점이 임피던스가 무한대가 되는 지점이고,
임피던스가 무한이라는것은 전류의 흐름을 방해하는 값이 무한이라는 것으로, 즉 회로가 끊어졌다는 의미이다.
제일 바깥쪽의 큰 원은 임피던스가 0이 되는 곳으로, 오른쪽에서 왼쪽으로 점이 이동할수록 임피던스의 값이 점점 작아진다는 의미이다.
또 임피던스가 0인 경우에는 전류의 흐름을 방해하는 값이 아예 없다는 말이기 때문에 short 된 상태라고 볼 수 있다.
그리고 스미스 차트 위에 한 점을 찍었을 때 그 점의 좌표 자체는 임피던스 값을 의미하고
위에서 스미스차트가 임피던스와 반사계수의 관계를 나타내는 차트라고 했는데
임피던스 점까지 원의 중심에서 떨어진 거리 r 을 원의 반지름 R 로 나눈 값이 반사계수의 크기, 그 점과의 각도가 반사계수의 위상이 된다.
반사계수(Γ) 크기 : r / R , 반사계수(Γ) 위상 : θ
다시 RF matching 이야기로 돌아와서...
RF matching이 필요한 이유는 효율적인 power 전달을 위해 반사계수를 줄이기 위해서이고
반사계수가 있다는 것은 말 그대로 내가 전달한 신호가 반사되었다는 것으로 RF reflection 이라고 한다.
반사계수는 원의 중심으로 부터 떨어질 수록 커지기 때문에 RF matching 과정을 스미스 차트에서 본다면
하나의 임피던스 점이 차트의 중심점으로 이동하는 과정이라고 할 수 있다.
위의 사이트가 많은 도움이 되었는데, 나는 아직... 공부를 더 해봐야 할 것 같다.
'self.반도체&전자회로 공부' 카테고리의 다른 글
| [반도체 직무] 반도체 R&D공정, 반도체연구소의 공정개발은 무슨일을 할까 (0) | 2023.09.23 |
|---|---|
| RF Matching System과 스미스차트에 대하여(Smith Chart) - 1 (0) | 2022.07.27 |
| 식각(etching) 공정에서 profile에 영향을 미치는 loading effect에 대해서 - 2 (0) | 2022.07.12 |
| 식각(etching) 공정에서 profile에 영향을 미치는 loading effect에 대해서 - 1 (1) | 2022.07.08 |
| 반도체 2 - DRAM 과 FLASH 의 차이점은 ? (0) | 2022.06.28 |



