도수분포표와 히스토그램
히스토그램은 데이터 분석을 함에 있어서 가장 기본으로, 그리고 많이 보는 그래프라고 생각한다.
그 히스토그램을 그리기 위해 필요한 데이터 표가 도수분포표이다.
도수분포표와 히스토그램에 대하여 공부해보자.
도수(frequency) 란?
자료를 크기순으로 배열했을 때 특정한 자료의 값이 몇 번 반복해서 나오는 경우, 그 값이 반복되는 횟수(빈도)를 말한다.
[1, 3, 4, 2, 3, 3, 2, 5, 6 ] 이라는 데이터가 있을때 '2'의 도수는 2, '3'의 도수는 3이 된다.
[M, XL, L, L, XXL, M] 이라는 데이터가 있을때 'M'의 도수는 2, 'XL'의 도수는 1이 된다.

이런 자료의 값과 도수를 정리한 표를 도수분포표(frequency table)라고 한다.
이 도수분포표에는 자료의 값, 도수 외에도 도수를 전체 관측값의 개수로 나눈 상대도수를 기입하는 경우가 많다.
[1, 3, 4, 2, 3, 3, 2, 5, 6 ] 이라는 데이터가 있을때 '2'의 도수는 2이고, '2'의 상대도수는 2/9 = 0.222... 가 된다.
[M, XL, L, L, XXL, M] 이라는 데이터가 있을때 'M'의 도수는 2이고, 'M'의 상대도수는 2/6 = 0.333... 가 된다.

이런 상대도수의 총 합은 당연히 1이 나오고
상대도수는 다른 두 종류의 자료의 분포를 비교할 때 많이 이용된다.
자료의 관측값의 개수가 많고 서로 다른 관측값들이 많은 자료에 대해서는 각각의 관측값에 대한 도수분포를 구하는것은 어렵다.(힘들다)
이런 경우에는 관측값을 몇 개의 계급으로 나누어 각 계급에 속하는 개수를 기록하는 것이 더 편리하다.
예를 들어, 강아지의 몸무게에 관한 분포에 대해 관심이 있다면
몸무게를 [~5kg 미만, ~10kg 미만, ~15kg 미만, 15kg 이상] 이렇게 4개의 계급으로 나누어 각 계급에 속하는 관측값의 개수를 세어 표를 만들 수 있다.
이런 경우 각 계급에 속하는 관측값의 개수를 계급의 도수라고 할 수 있다.

이런 계급의 수를 정할때,
계급의 수가 너무 많으면 한 눈에 들어오지 않으니 자료를 요약하지 않은것과 마찬가지이고
반대로 너무 적어 너무 큰 단위로 구분이 된다면 오히려 나눈 의미가 없어지고 많은 정보가 손실될 수 있다.
일반적으로 계급의 수는 관측값의 개수에 따라 대략 6~20 개 정도로 한다.
이렇게 계급으로 나누어 도수분포표를 작성하게 되면
데이터가 많은 경우에 그 데이터 분포의 대략적인 형태를 쉽게 알 수 있다.
위의 예시 표를 보면 "5~10kg 사이의 강아지가 가장 많구나" , "10kg 미만의 강아지가 절반이 넘네" 등의 정보를 얻을 수 있다.
주어진 자료를 도수분포표로 정리한 뒤에는 자료의 분포 상태를 한눈에 알아볼 수 있도록 히스토그램을 그린다.
히스토그램에서 각 계급에 대한 직사각형의 밑변은 계급의 폭이 되고, 높이는 도수밀도이다.
결국 히스토그램에서 각 직사각형의 면적은 바로 그 계급의 도수를 나타내는것이다.
이 말은 모든 직사각형을 더하면 전체 도수 즉, 총 데이터의 크기를 나타내는 값이다.
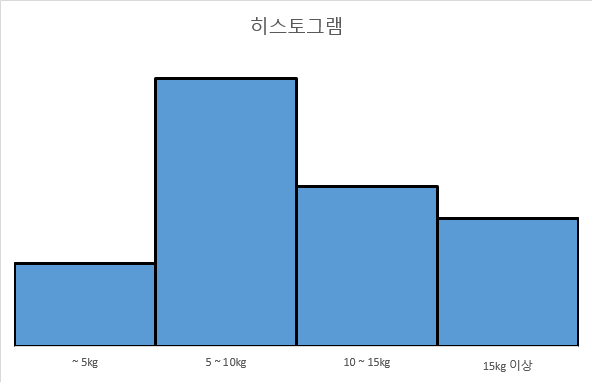
보통 각 계급의 폭은 동일하게 나누기 때문에 그래프의 높이로 비교를 하는 경우가 많다.
만약 계급의 폭이 동일하지 않은 경우 면적을 비교하여야 한다.
'self.statics' 카테고리의 다른 글
| [Statics] 통계적 추론 - 추정에 대하여 (0) | 2023.05.30 |
|---|---|
| [statics] 전확률의 정리와 베이즈의 공식 Bayes' formula (0) | 2022.08.16 |
| [Statics] 사분위수와 상자그림 boxplot (0) | 2022.07.23 |
| [Statics] 표본평균의 분포 - 중심극한 정리 (0) | 2022.07.17 |



