사분위수와 상자그림 boxplot
앞 글의 히스토그램에 이어 상자그림도 데이터 분석을 하면서 자주 그리게 되고, 자주 사용하게 되는 그래프이다.
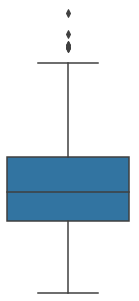
이전에 seaborn 으로 그렸던 box plot이다. 이 그래프의 각 구성요소가 무엇을 의미하는지 상자그림에 대해서 공부해보자.
상자그림은 사분위수를 그래프로 표현한 것이다. 사분위수에 대해 말하기 전에 수치요약에 대해서 먼저 보면
five number summary
자료를 크기 순으로 나열 후 4등분 했을 때 경계가 되는 수치.
최소값, 첫 번째 4등분점(제 1분위수), 두 번째 4등분점, 세 번째 4등분점(제 3분위수), 최대값 이렇게 다섯개의 수치라서 다섯 수치요약이라고 한다.
두 번째 4등분점은 중위수 = median 이라고 하며 M으로 표시한다.
첫 번째와 세 번째 4등분점은 각각 제 1분위수, 제 3분위수라고 하며 Q1, Q3 로 표시한다.
중위수와 사분위수를 쉽게 찾기 위하여 관측값의 깊이 개념을 사용한다.
관측값의 깊이(depth)는 데이터를 크기 순서로 나열했을 때 중앙의 왼편에 있을 때는 왼쪽으로부터, 오른편에 있을 때는 오른쪽으로부터의 누적도수이다.
3 9 14 22 39 41 56 63 79 97
이런 데이터가 있다고 하자. 10개의 관측값이 있는 자료에서 3과 97은 깊이가 1이 된다.
9와 79는 깊이가 2가 되는것이다.
여기서, 중위수와 사분위수는 다음과 같은 깊이를 갖는 자료점이다.

예시로 나열한 10개의 데이터에서 보면 중위수의 깊이는 5.5 가 되고, 사분위수의 깊이는 3이 된다.
그러므로 중위수는 다섯 번째 관측값인 39와 여섯 번째 관측값인 41을 합하여 2로 나눈 40이 되는것이고
제 1사분위수 Q1은 왼쪽에서 부터 세 번째 값인 14, 제 3사분위수 Q3는 오른쪽에서 부터 세 번째 값인 63이 된다.
상자그림을 보면 분포의 중심위치, 이상치, 분포의 모양 등의 특성을 알아낼 수 있다.
만약 여러개의 상자그림을 함께 그려 비교하려 한다면 동일한 척도의 수직선에 그려야 함을 주의해야 한다.
box plot 작성 순서
1. 다섯 수치요약을 구한다.(minimum, Q1, M, Q3, Maximum)
2. 두 사분위수(Q1, Q3)에 해당하는 수직선 상의 위치에 네모형 상자의 양 끝이 오도록 상자를 그리고, 그 상자 안에서 중위수(M)에 해당하는 위치에 선을 긋는다.

3. 두 사분위수의 차이 IQR = Q3 - Q1을 계산하고 두 개의 inner fence값 IL, IU 와 두 개의 outer fence값 OL, OU를 계산한다. 여기서 IQR은 사분위범위라고 한다.

4. 양쪽 inner fence의 안에 있거나 이 값과 같은 관측값 중 가장 가까운 관측값을 각각 찾아낸다.
이 관측값을 인접값이라 하고 AL과 AU로 표시하고 상자의 양 끝에서 두 인접값 AL, AU의 위치까지 선으로 연결한다.

5. inner fence와 outer fence 사이에 관측값이 있으면 그들을 이상치로 분류하고 그 위치에 * 표시를 한다.
만약 outer fence 밖에도 관측값이 있다면 그것들은 극단 이상치(extreme outlier)로 분류하고 그 위치에 'o' 표시를 한다.

'self.statics' 카테고리의 다른 글
| [Statics] 통계적 추론 - 추정에 대하여 (0) | 2023.05.30 |
|---|---|
| [statics] 전확률의 정리와 베이즈의 공식 Bayes' formula (0) | 2022.08.16 |
| [Statics] 도수분포표와 히스토그램 (0) | 2022.07.20 |
| [Statics] 표본평균의 분포 - 중심극한 정리 (0) | 2022.07.17 |



