베이즈의 공식 Bayes' formula
베이즈(Bayes)의 공식은 영국의 수학자이며 장로 교회 목사였던 베이즈에 의해 만들어졌다.
베이즈의 공식은 예전에 파이썬으로 알고리즘 공부를 할 때 처음 들어보게 된 것이었는데 더 알아보자.
여러 대의 기계가 동일한 제품을 생산하는데, 이에 대한 불량률이 각 기계별로 주어져 있다고 가정하자.
만약 어떤 특정한 기계에서 생산된 제품 중 임의로 한 개의 제품을 뽑아내는 실험을 한다면,
우리의 관심은 특정한 기계가 선택되었다는 조건 아래에서 뽑은 제품이 불량품이 될 확률이다.
이러한 확률을 바로 그 기계에서 생산된 제품의 불량률이라고 할 수 있다.
베이즈의 공식은 이 반대의 문제를 해결하는데 도움을 줄 수 있다.
즉, 어느 기계에서 생산되었는지 모르는 한 제품을 임의로 뽑았는데 그것이 불량품이라면
과연 이 불량품이 어느 기계에서 생산된 것인가 하는 문제를 다루는 데 효과적이다.
1. 정의
표본공간이 n개의 사상 B₁, B₂, ..., Bn 에 의해 분할되어 있고, 모든 i = 1, 2, ..., n 에 대하여 P(Bi)가 0이 아니라면
임의의 사상 A에 대해 다음의 식이 성립한다.
- 전확률의 정리

- Bayes의 공식
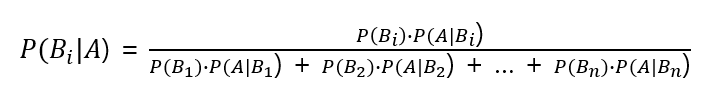
2. 예시
예시를 통해 쉽게 이해해보자.
장난감 가게에 있는 전체 장난감 중 50%는 한국에서 생산된 것이고, 이 중의 15%는 로봇이다.
전체 장난감 중 30%는 일본에서 생산된 것이고, 이 중의 40%는 로봇이다.
전체 장난감 중 20%는 중국에서 생산된 것이고, 이 중의 60%는 로봇이다.
임의로 하나의 장난감을 골랐을 때 고른 장난감이 다음과 같이 될 확률은 ?
1) 로봇일 확률
2) 로봇이라는 조건 아래 그 로봇 장난감이 일본에서 생산되었을 확률
1) 로봇일 확률
고른 장난감이 로봇인 경우는 한국의 로봇이거나, 일본의 로봇이거나, 중국의 로봇이거나 이 세 가지 경우 중 하나일 것이다. 각각의 사상을 다음과 같이 정의해보자.

이것을 벤 다이어그램으로 나타내보자.

그러면 A = (A∩B₁) ∪ (A∩B₂) ∪ (A∩B₃) 이 되고,
(A∩B₁) 와 (A∩B₂), (A∩B₃)은 서로 배반적이므로
P(A) = P(A∩B₁) + P(A∩B₂) + P(A∩B₃)
= P(B₁)·(A│B₁) + P(B₂)·(A│B₂) + P(B₃)·(A│B₃)
= (0.50)(0.15) + (0.30)(0.40) + (0.20)(0.60)
= 0.315
2) 로봇이라는 조건 아래 그 로봇 장난감이 일본에서 생산되었을 확률
P(B₂│A) = P(A∩B₂) / P(A) = P(B₂)·(A│B₂) / P(A)
= (0.30)(0.40) / 0.315 = 0.381 (반올림)
이 예시의 경우 표본공간이 B₁, B₂, B₃ 라는 세 사상에 의해 분할 되었다고 할 수 있다.
B₁, B₂, B₃ 는 서로 배반적이며 B₁ ∪ B₂ ∪ B₃ 가 표본 공간이 되면 B₁, B₂, B₃를 표본공간의 분할이라고 한다.
이런 경우 임의의 장난감을 골랐을 때, 그 장난감은 B₁, B₂, B₃ 중 하나에만 속하게 되고 다음의 식이 성립한다.
P(A) = P(B₁)·(A│B₁) + P(B₂)·(A│B₂) + P(B₃)·(A│B₃)
이 결과를 일반화한 것을 전확률의 정리라고 한다.
전확률의 정리에 의해 사상 A가 일어날 확률을 구하면, 고른 장난감이 로봇이라는 조건 아래 그 로봇이 일본 제품일 확률은 위의 예제에서 구했듯이 다음의 식으로 구할 수 있다.
P(B₂│A) = P(B₂)·(A│B₂) / P(A)
* P(A) = P(B₁)·(A│B₁) + P(B₂)·(A│B₂) + P(B₃)·(A│B₃)
이 결과를 일반화 한 것을 베이즈의 공식이라 한다.
'self.statics' 카테고리의 다른 글
| [Statics] 통계적 추론 - 추정에 대하여 (0) | 2023.05.30 |
|---|---|
| [Statics] 사분위수와 상자그림 boxplot (0) | 2022.07.23 |
| [Statics] 도수분포표와 히스토그램 (0) | 2022.07.20 |
| [Statics] 표본평균의 분포 - 중심극한 정리 (0) | 2022.07.17 |



