다이오드의 평형상태 (V = 0)
이전 pn접합의 특성 글에서 공부했듯이 외부 전압이 걸리지 않을 경우 pn 접합의 주위에는 공간전하영역이 형성되고, 이 영역에는 캐리어의 밀도가 아주 작다. (공핍근사, depletion approximation)
p형 반도체 영역에서는 정공이 다수캐리어로서 그 밀도는 어셉터 원자의 밀도와 같은 N_a 이고 소수캐리어인 전자의 밀도는 (n_i)²/N_a 이다.
n형 반도체 영역에서는 전자가 다수캐리어로서 그 밀도는 도너 원자의 밀도와 같은 N_d 이고 소수캐리어인 정공의 밀도는 (n_i)²/N_d 이다.

pn 접합을 그림으로 나타낸 것이다. 접합부에서부터 각각 x_p0 , x_n0 까지가 각각의 공간전하영역으로 표시한 것이다.
공간전하영역과 각 반도체 영역의 경계는 명확하다고 가정한다.
p형 반도체 쪽의 공간전하영역의 전하밀도는 -qN_a 이고, n형 반도체 쪽의 공간전하영역의 전하밀도는 qN_d 이다.
전하보존법칙에 의해서 아래 식이 만족된다.

그림에도 나와있듯이 이 공간전하영역에 의해 전기장이 발생되는데 전기장은 아래 식으로 주어진다.

p형과 n형 반도체 영역에서는 전기적으로 중성이므로 전기장은 0 이 된다.
반면에 공간전하영역에서는 이온화된 어셉터와 도너 원자들에 의해 전기장이 발생한다.
즉, p형 반도체의 공간전하영역인 -x_p0 ~ 0 의 영역에서의 전기장은 아래 식으로 주어진다.

이 식에서 경계조건 E(-x_p0) = 0 이므로

로 된다.
동일하게 n형 반도체의 공간전하영역인 0 ~ x_n0 영역에서의 전기장은 아래와 같다. 두 식 모두 위의 그래프에 표현되어 있다.

평형상태(V=0)에서는 확산전류와 드리프트 전류는 동일하다. 이 조건을 전자의 경우에 적용하여 표현하면 아래와 같다.

앞 글에서 말했던 아인슈타인 관계식을 적용하여 다시 정리하면 아래와 같다.

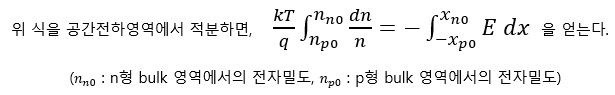

따라서 내부 포텐셜 V_B는 왼쪽항을 적분 한 값으로 아래와 같이 구해진다.
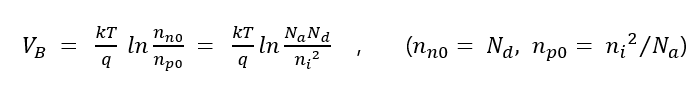
공간전하영역에 있는 임의의 위치 x에서의 포텐셜을 구해보자.
위에서 어떤 구간에서 내부포텐셜을 어떻게 구하는지 알아보았다. x_1 ~ x_2 영역에서의 내부포텐셜은 아래와 같다.
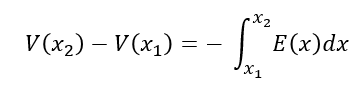
먼저 -x_p0 < x < 0 의 영역에서의 포텐셜은 아래와 같이 주어진다.
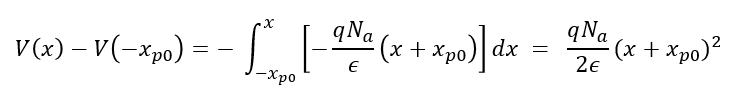
p형 반도체 경계에서의 포텐셜 V(-x_p0) = V_p 이므로 (경계조건) 아래와 같이 구해진다.
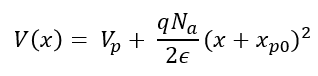
같은 방법으로 0 < x < x_n0 의 영역에서의 포텐셜을 구하면 아래와 같다. 이 영역에서의 경계조건은 V(x_n0) = V_n 이다.
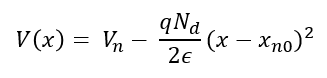
위 식들의 표현에서는 x_n0, x_p0 의 값들이 주어지지 않았는데 이는 pn 접합의 전 영역에서 전하가 보존되어야 한다는 조건에서 구할 수 있다. (charge neutrality)
p형과 n형 반도체 영역은 전기적으로 중성이므로, 공간전하영역에서의 전하의 보존에서
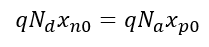
가 만족되어야 한다.
그리고 접합부분(x=0)에서 포텐셜은 연속이어야 한다는 조건도 만족시켜야 한다. 위에서 구한 각각의 p형, n형 반도체에서의 포텐셜 식에 x=0 을 대입하면 그 둘은 같은 값이어야 한다는 말이다.
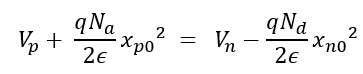
공간전하영역에서의 전하의 보존되어야 한다는 조건과, 접합부분에서 포텐셜이 연속이어야 한다는 조건을 조합함으로써 x_p0 와 x_n0를 각각 구할 수 있다.
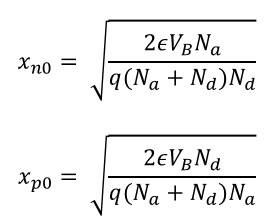
공간전하영역의 폭 x_d 은 x_p0 + x_n0 이다.
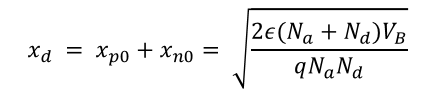
그리고 x_p0 이나 x_n0을 알고 있으니 접점(x=0)에서의 전기장(E)을 구할 수 있다.
위에서 구했던 전기장 식에 x=0을 넣고 x_p0 또는 x_n0 값을 대입하면
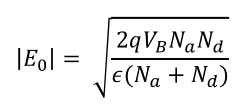
와 같이 구할 수 있다.
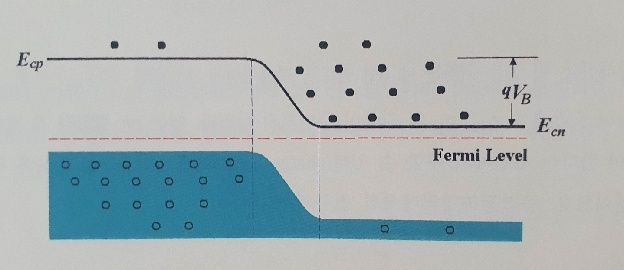
평형상태(V=0)에서의 에너지준위 그림이다. p형과 n형 반도체의 전도대의 에너지 차이가 q*V_B 로 주어진다.
p형과 n형 반도체의 캐리어들의 알짜 이동이 이 내부포텐셜이 장벽이 되어 평형상태에 도달하게 된다.
그리고 이에 따라 평형상태에서의 p형과 n형 반도체 영역의 Fermi 준위는 동일해진다.
이렇게 pn 접합에서 p형과 n형 반도체 영역의 Fermi 준위는 동일해지는 성질을 이용함으로써 내부포텐셜을 구할 수 있다.
n형과 p형 영역에서의 전자와 정공의 밀도에 대한 식을 평형상태에서 표현하면 아래와 같다. 두 식에서 Fermi 준위(E_F)가 동일하다.
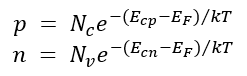
두 식을 나누고(p/n), ln을 취한 후 q*V_B = E_cp - E_cn 을 사용하여 내부포텐셜을 구하면 결국 위에서 구한 내부포텐셜과 동일한 결과가 나오는 것을 볼 수 있다.

'과학도를 위한 반도체와 전자회로의 기초' 책을 공부하여 작성 하였습니다.
'self.반도체&전자회로 공부' 카테고리의 다른 글
| [pn접합의 특성] 다이오드의 정전용량 (0) | 2022.03.26 |
|---|---|
| [pn접합의 특성] pn접합의 물리적 성질2, 다이오드 전류-전압 특성 (0) | 2022.03.25 |
| [pn접합의 특성] pn 접합이란? 다이오드 (0) | 2022.03.23 |
| [반도체의 특성] 캐리어에 의한 전류밀도 (0) | 2022.03.22 |
| [반도체의 특성] 반도체 캐리어(Carrier) 밀도_2 (0) | 2022.03.21 |



